Everyone’s heard the wisdom that you can’t compare apples and oranges, or some version of the saying from around the world. According to Wikipedia, variously: apples and pears; cabbages and carrots; potatoes and sweet potatoes; even grandmothers and toads (that last one's Serbian, if you were wondering).
This is often extrapolated to not adding apples and oranges (or grandmothers and toads), when teaching the fundamentals of Units. When doing calculations, it’s ok to multiply or divide apples and oranges (e.g. ratio of apples to oranges), but not ok to add them - the overriding rule is: “you can only add together items of the same unit”.
But wait, surely we can sometimes add together apples and oranges. What if we’re counting the number of pieces of fruit in a fruit bowl? Of course, you’re unlikely to be modelling the availability of fruit in your office in the near future, but there are plenty of real world examples where adding things of a different unit can be useful.
As an example, take a typical telecoms business, which we’ll refer to as an MSO - multi-service operator. The MSO offers several products including TV, telephony and broadband. Some customers take a single product, some several. Individual customers are usually referred to somewhat impersonally as RGUs (Revenue Generating Units) and it’s interesting to the MSO how many of these they have, and how much they spend.
But the MSO also needs to know about individual products, or subscriptions, and how they’re performing. So any modelling of the MSO’s business will need to deal with TV, telephony and broadband separately. In each of those parts of the model, we’ll use specific units like TV subscription, Telephone subscription, and Broadband subscription - this is sensible, as we’ll be dealing with logic that isn’t relevant to the other parts.
But inevitably the MSO will want to know the total number of subscriptions being sold by the business, along with other KPIs like number of subscriptions per RGU, which requires us to add together the three different Units. Intuitively, this isn’t a problem: we can rationalise that if we add together the three specific subscription units, we’ll end up with some value that has a unit of, simply, Subscription.
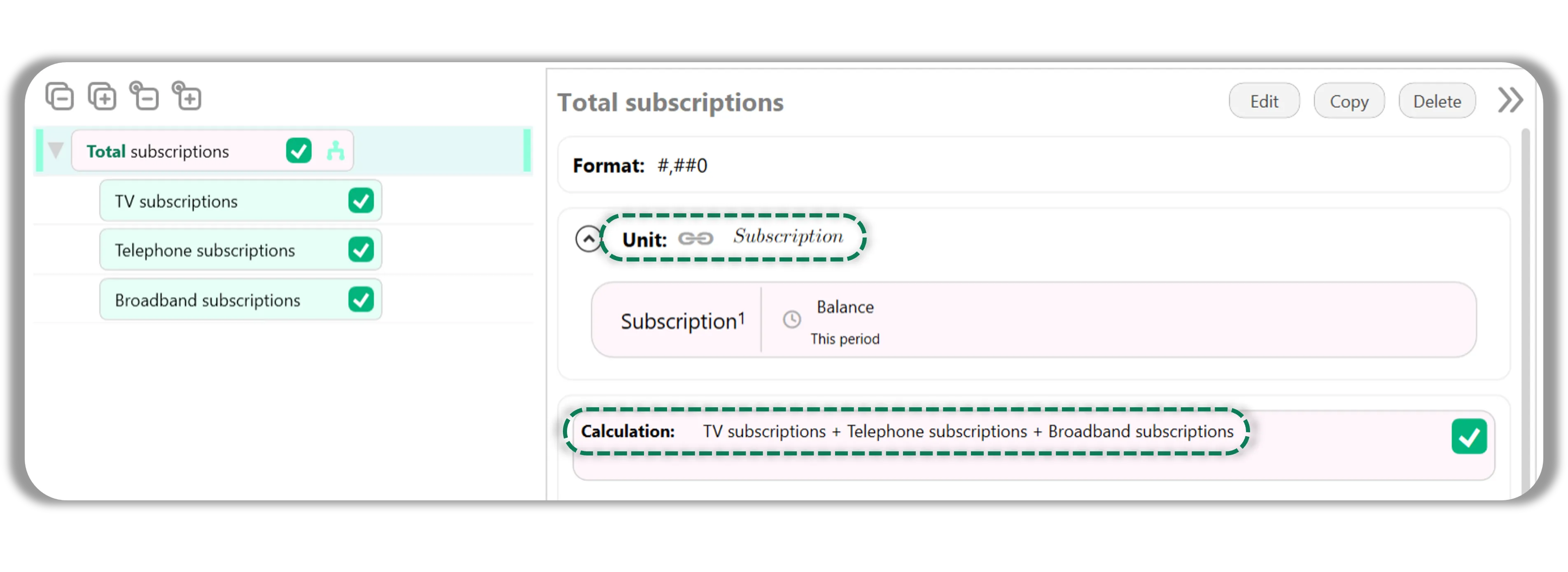
And you’ll be pleased to know that in Models from Taglo, this process is just as straightforward. Units in Models are based on Tags, and Tags in Taglo are hierarchical. The definition of our Unit Tags is shown below:
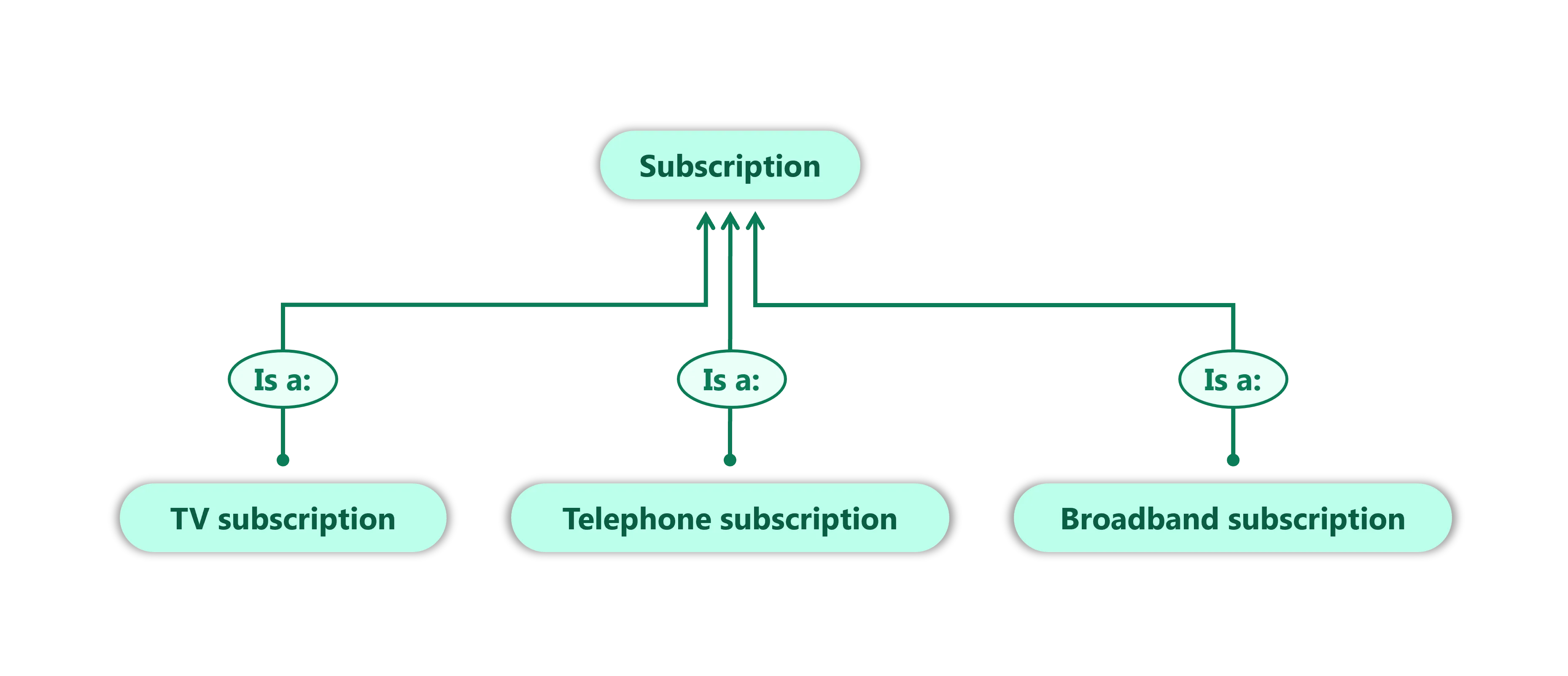
As soon as you add any of these Units together, Models will see that they are of a different Unit, and try to find a common ancestor - in this case, Subscription.
The screenshot below shows what this looks like in Models. Job done!